Keywords

• Baseline removal
• Smooth
• curvilinear integral
  • Simpson rule
  • Trapezoidal rule
• Application background: XRD, DEMS…

TOC

• • Keywords
• TOC
• EKL Chaos 1264
  • 1️⃣import and load data (smooth is defined):
  • 2️⃣make comparison of 3 different results:
  • 3️⃣'Baseline removal' explained
  • 4️⃣'Smooth' : What's the most proper number for a WindowSize?
  • 5️⃣ curvilinear integral
  • 6️⃣Conclusion

EKL Chaos 1264

↩️
Let's get right to the topic. In order to show the data you got in a eye-catching and clear way, some pretreatments need to be done first.
Present characterization technologies mainly show the results of tests by catching signal. And those signal of samples are commonly composed of noise , signal of the sample itself and signal of the sample table (or the machine). For removing invalid information as much as possible, some signal processing methods have to be implemented. 'Baseline removal' and 'Smooth' are two of them.

Here's the entire process:

• load the data --- txt file.
  • you can plot it first to see whether the characteristic peaks are clear or not.
  • do the Baseline removal.
  • smooth the line.
  • mark the peaks and label them.

1️⃣import and load data (smooth is defined):

↩️

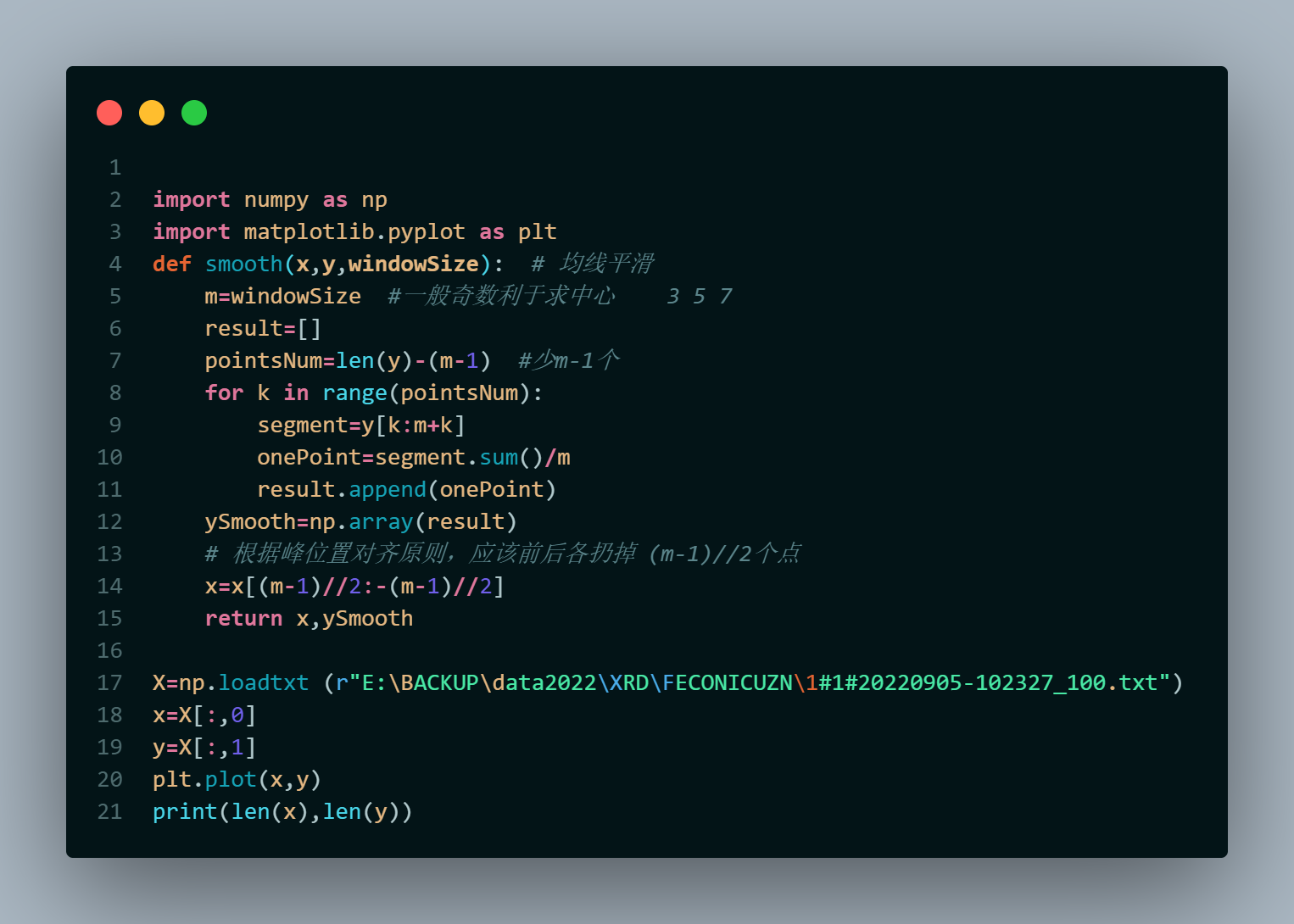
Figure 1

2️⃣make comparison of 3 different results:

↩️

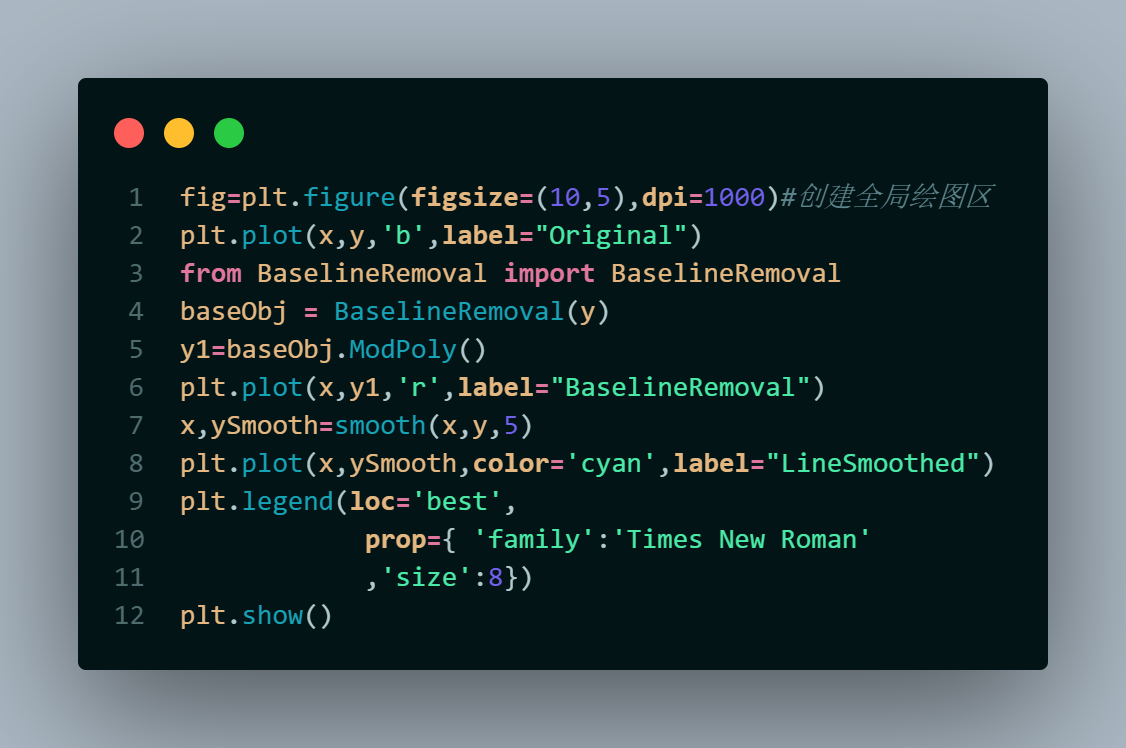
Figure 2

Figure 3

3️⃣'Baseline removal' explained

↩️
There are many ways to remove the baseline, and the simple one is to average it. There're already the library that you can import directly---'BaselineRmoval'. Sometimes at certain positions, signal is quite high than other positions around. And it's possibly caused by the sample table or the substances ain't belong to the sample.

4️⃣'Smooth' : What's the most proper number for a WindowSize?

↩️
As you can see in Figure 1, there's a variable needed to be defined---WindowSize. As its name implies, there's a window for the smooth process. So how can we define it to get the job done properly? Therefore, we digged the answer here:

• We defined the different scale of windowsizes and the length of the data: len(x)=2751
  
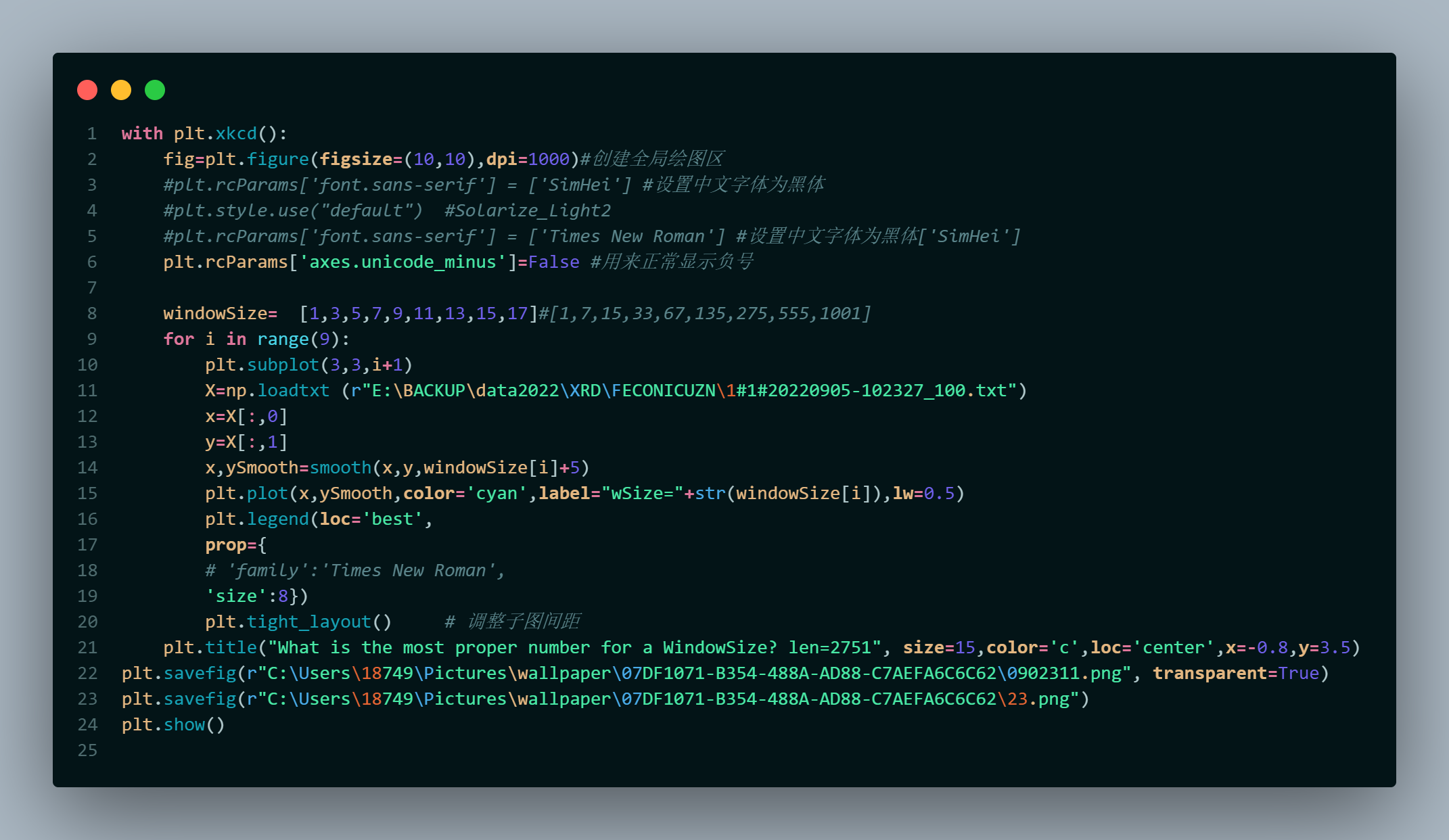
  Figure 4

• Here're plots that we got:

  • [1,3,5,7,9,11,13,15,17]

Figure 5 WindowSize=[1,3,5,7,9,11,13,15,17]

• [1,7,15,33,67,135,275,555,1001]

Figure 6 WindowSize=[1,7,15,33,67,135,275,555,1001]

As you can clearly see in the plots above, the quite big windowsizes smooth the line too much to get all the right information-- peaks. However, when the number goes small, it seems that results are not widely different from each other.

5️⃣ curvilinear integral

↩️
Sometimes the squals of the area in the plot need to be calculated. There're two main methods out there.

• Simpson rule
• Trapezoidal rule
  
  
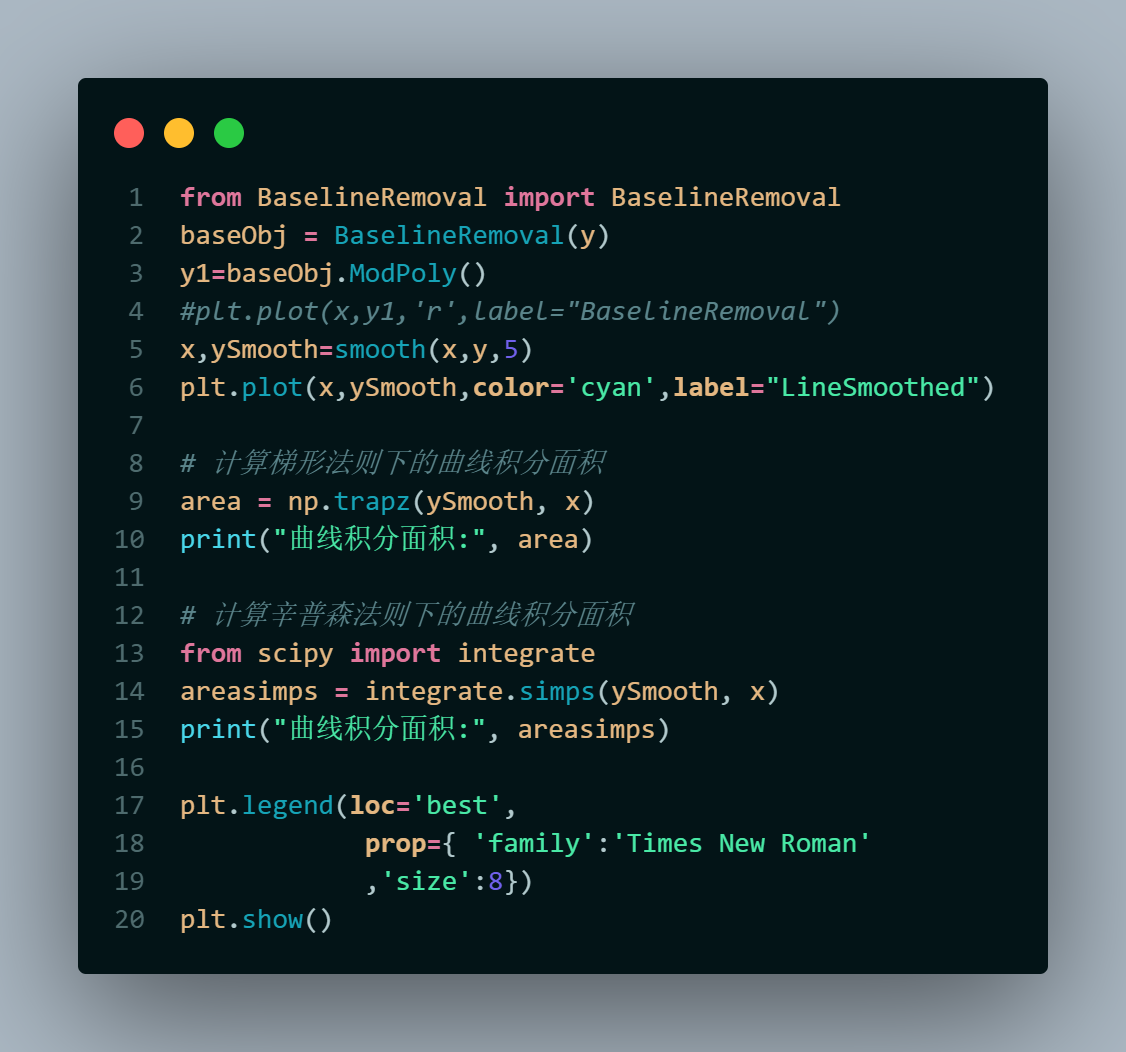
  Figure 7 curvilinear integral code&results

6️⃣Conclusion

↩️

• 'Baseline removal' is extremely simple. Just import and apply it.
• In terms of 'Smooth' , the number of the WindowSize matters. It's somthing to do with the scale of the data you process. Bur remember don't set it too big. 3, 5, 7 are recommended. Even though don't forget to compare the results to the original one eventrually, in case you lost some infomation which is quite of importance.

Till next , stay safe and stay hydrated!